Contents.
1. A relationship
Our motivation on this article is the following relation.
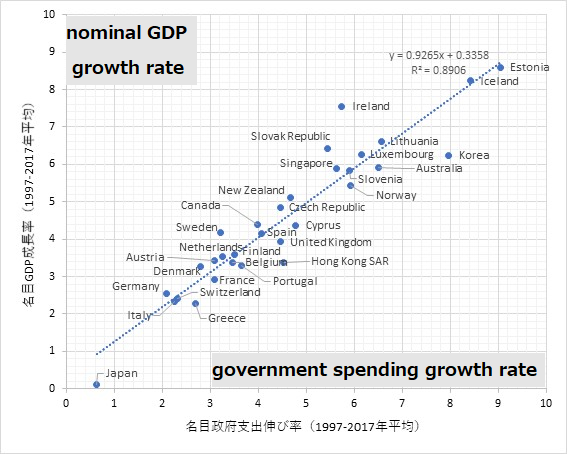
This figure shows a relation of growth rates between nominal GDP and government spending. Data is of 31 countries, and is 20-years averaged. This figure shows very impressive relation. Growth rates of nominal GDP (y-axis) is proportional to those of government spending (x-axis). Ranges of x- and y-axes are from 0% to 10%.
The original figure is from the following tweet.
以下の散布図の解釈について補足。
— ParkSJ 朴勝俊🌹GND 脱原発!グリーン・ニューディール (@psj95708651) November 8, 2020
長期は生産関数でGDPが決まるなら、仮にY=A×K^β×L^(1-β)【Aは技術、Kは資本、Lは労働】としたとき、小文字をそれぞれの成長率として、
y=a+βk+(1-β)l 【エル】
となる。この式に政府支出の伸び率gは含まれない。従って理論上、yとgの相関はゼロのはず。 pic.twitter.com/oauNRLpFuE
We do not know whether this figure is included in a published paper or not.
2. Our derivation
This relation can be described as,
- dY/Y = dG/G,
where Y is the nominal GDP, and G is the government spending, and dA/A is the growth rate (= (A2-A1)/A1).
This relation can be given from the quantity equation.
- Y=MV,
where M is the amount of money supplied to the money circulation, and V is the circulation velocity of money. This equation can be transformed, as follows,
- dY/Y = dM/M + dV/V.
This equation indicate that growth rate of nominal GDP is the sum of dM/M and dV/V. Note that this equation is an approximation equation, and can be applied when these variations (growth rates) are roughly less than 0.1.
When dV/V=0 (dV/V~0) and M=aG (`a' is a constant value), we obtain the observed relation.
- dY/Y = dG/G
3. dV/V=0 and M=aG
Here, dV/V=0 and M=aG are from our quantitative view on the money circulation (`A three-piece set for understanding the money circulation'). We integrated the circular flow diagram, a definition of nominal GDP, and the quantity equation (Fisher's equation of exchange) for quantitatively understanding the money circulation.
In this integration, we obtained M=G+I. We just set M=G+I=aG for simplification. Values of `a' could be different in different countries.
As for dV/V=0, this means that variation of V is much less than that of M during long time. From our quantitative view, we obtain V=Y/(G+I)=1/(1-β), where β is the average propensity to consume. We can increase government spending and nominal GDP. However, β in nominal GDP is relatively steady in each country. If drastic change happens in a country, β will change greatly.
Our original article in Japanese, '【貨幣循環】歳出伸び率とGDP成長率の関係(MVとMの各変化率の関係)'
Link page: Contents for money circulation




No comments:
Post a Comment